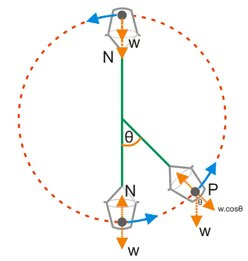
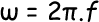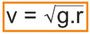Dinamika Partikel

DINAMIKA PARTIKEL

Dinamika partikel adalah cabang mekanika yang mempelajari gerak suatu partikel dengan meninjau penyebab geraknya. Gerak dari suatu partikel dipengaruhi oleh sifat-sifat dan susunan benda lain yang ada disekitarnya. Persoalan pengaruh lingkungan yang mempengaruhi gerak suatu partikel telah dipecahkan oleh Issac Newton (1642-1727) yang digambarkan dengan menggunakan hanya tiga hukum sederhana yang dinamakan dengan hukum Newton tentang gerak.

11.      Hukum I Newton

Hukum pertama Newton menyatakan bahwa sebuah benda dalam keadaan diam atau bergerak dengan kecepatan konstan akan tetap diam atau bergerak dengan kecepatan konstan kecuali ada gaya eksternal yang berpengaruh pada benda tersebut.

Kecenderungan dari sifat benda seperti itu disebutkan bahwa benda mempunyai kelembaman, sehubungan dengan itu, hukum I Newton sering disebut hukum kelembaman/inersia.

Hukum pertama Newton tidak membuat perbedaan antara benda yang diam dengan benda yang bergerak dengan kecepatan konstan, pertanyaan apakah suatu benda sedang diam atau bergerak denan kecepatan konstan bergantung pada kerangka dimana benda tersebut diamati. Hukum pertama Newton berlaku pada kerangka acuan yang inersial, yaitu kerangka acuan yang bergerak dengan kecepatan konstan atau diam.

2. Hukum II Newton

Pada hakikatnya, hukum pertama dan hukum kedua Newton dianggap sebagai definisi gaya. Gaya adalah suatu pengaruh pada sebuah benda yang menyebabkan benda mengubah kecepatannya atau mengalami percepatan. Arah gaya sama dengan arah pecepatan yang ditimbulkan oleh gaya tersebut jika gaya itu adalah satu-satunya gaya yang bekerja pada benda yang bermassa. Massaadalah sifat intrinsik sebuah benda yang mengukur resistansinya terhadap percepatan. Jika gaya F dikerjakan pada benda bermassa m_1, dan menghasilkan percepatan a₁, maka

F = m₁a₁

Jika gaya yang sama dikerjakan pada benda kedua yang massanya m₂ dan menghasilkan percepatan a₂ maka

F = m₂a₂

Dengan menggabungkan kedua persamaan diatas kita dapatkan

F = m₁a₁= m₂a₂

Atau

Hubungan tersebut dapat digunakan untuk menentukan perbandingan massa-massa partikel yang diukur dari pengukuran yang terjadi pada m₁ dan m₂. Jika m₁ dipilih sebagai satuan massa maka massa partikel lain dapat ditentukan. Massa dari benda yang ditentukan dengan cara tersebut dinamakan dengan perbandingan massa Inersia

Dari definisi tentang gaya dan massa diatas, Newton menyatakan dalam hukum II Newton, yaitu “laju perubahan momentum benda terhadap waktu berbanding lurus dengan resultan gaya yang bekerja pada benda dan besarnya sama dengan gaya tersebut

Dari persamaan diatas dapat dilihat bahwa percepatan berbanding lurus dengan gaya yang bekerja dan berbanding terbalik dengan massa benda. Atau dapat dikatakan besar percepatan benda bila dikalikan dengan massanya akan sama dengan besar gaya yang bekerja pada benda tersebut.

Momentum sebuah partikel secara matematis didefinisikan sebagai hasil kali massa dengan kecepatan, sedangkan secara fisisnya momentum sebuah partikel dianggap sebagai ukuran kesulitan untuk mendiamkan suatu benda.

Hukum kedua Newton dalam kaitannya dengan momentum dapat dituliskan

3. Hukum III Newton

Hukum ketiga Newton kadang-kadang dinamakan hukum interaksi atau aksi reaksi. Hukum ini menggambarkan sifat penting dari gaya, yaitu bahwa gaya selalu terjadi bersama-sama.

Misalkan F₁₂ adalah gaya yang dikerjakan oleh partikel 1 pada partikel 2, dan F₂₁ adalah gaya oleh partikel 2 pada partikel 1.

Persamaan ini dikenal dengan Hukum kekekalan momentum, dengan penjelasan “jika resultan gaya eksternal yag bekerja pada sistem sama dengan nol, maka vektor momentum total sistem tetap konstan.

Momentum Sudut

Pada gerak rotasi momen inersia I merupakan analogi dari massa m dan kecepatan sudut merupakan analogi dari kecepatan linear v, maka rumus momentum sudut dapat ditulis sebagai

L = r x p

= r. p sin q

= r . m

= r. mwr

= mr²w

Momentum sudut merupakan besaran vektor. Arah momentum sudut mengikuti aturan tangan kanan, yaitu apabila keempat jari tangan kanan (selain jempol) dikepalkan mengikuti arah rotasi benda, maka jempol yang teracung menunjukkan arah momentum sudut.

Hubungan momentum sudut dengan momen gaya

Mengingat hubungan impuls dengan momentum Fdt = dp pada gerak linear, maka secara analogi, pada gerak rotasi diperoleh

Ndt=dL

Keterangan :

L = Momentum sudut (kg.m²/s)

I = Momen inersia (kg.m²)

N = Momen gaya (N.m)

Kekekalan Momentum Sudut

F = m.a

Jika SF= 0 maka dp = 0 atau p = konstanta hukum kekekalan momentum linear dari persamaan diatas dapat diturunkan kaitan momentum sudut dengan momen gaya yaitu:

Jika t = 0 maka L= konstan atau dengan kata lain momentum sudut sistem kekal. Dari persamaan diatas kita peroleh jika tidak ada momen gaya luar yang bekerja pada sistem , maka momentum sudut L konstan, atau dengan kata lain dapat disebut prinsip kekekalan momentum sudut. Secara matematis, kekekalan momentum sudut ditulis sebagai

L₁=L₂

GAYA FUNGSI POSISI

Usaha dan Energi

Konsep usaha yang dikerjakan oleh sebuah gaya, energi potensial dan energi kinetik sangat penting dalam masalah dinamika. Usaha yang dilakukan pada sebuah partikel dw oleh sebuah gaya hingga partikel tersebut berpindah sepanjang lintasan sejauh dr dinyatakan:

Persamaan diatas juga dapat dituliskan dalam bentuk Karena adalah energi kinetik partikel maka, diketahui bahwa besarnya usaha yang dikerjakan pada sebuah partikel sama dengan perubahan energi kinetik partikel. Usaha dw bernilai negatif, ketika momentum partikel yang bergerak berlawanan arah dengan gaya yang bekerja, sehingga usaha akan mengurangi energi kinetik partikel.

Usaha oleh gaya F yang mengalami pergeseran dari titik ke titik dinyatakan dalam integrasi :

Usaha adalah jumlah dari perubahan energi kinetik partikel

Fungsi dinamakan energi potensial. Integral dari usaha

Untuk gerak satu dimensi jika menimbulkan gaya hanya fungsi dari posisi kemudian jumlah dari energi kinetik dan energi potensial adalah konstanta dan usahanya sama dengan nol, ketika partikel tersebut bergerak mengelilingi suatu lintasan tertutup dan kembali ke posisi semula, contohnya gaya pegas dan gaya gravitasi. Sedangkan gaya desipatif adalah gaya yang usahanya tidak sama dengan nol dan bergantung pada lintasan, contohnya gaya gesek.

Contoh problem gaya konservatif

1.      Gaya pegas

2.       gaya konservatif

2. Gaya Gravitasi

Dulu, diasumsikan bahwa g adalah konstan. Kenyataannya, gaya gravitasi antara dua pertikel berbanding terbalik dengan kuadrat jarak antara keduanya (Hukum Gravitasi Newton).

dimana G adalah konstanta gravitasi Newton, M adalah massa bumi, dan r adalah jarak antara pusat bumi dengan benda. Dapat didefinisikan bahwa gaya sama dengan besarnya ketika suatu benda berada pada permukaan bumi, sehingga , adalah percepatan gravitasi pada permukaan bumi. R adalah jari-jari bumi (diasumsikan bola),. Dengan mengabaikan beberapa gaya seperti hambatan udara.

Misalkan sebuah benda dilempar ke atas dengan laju awal diatas permukaan bumi, dengan. Untuk penyelesaian, diperoleh hubungan,

GERAK KARENA GAYA SEBAGAI FUNGSI WAKTU ( Konsep Dari Impuls)

Jika gaya bekerja pada sebuah partikel , yang diketahu secara jelas sebagai sebuah fungsi waktu, maka persamaan gerak, untuk massa konstan adalah :

Persamaan tersebut bisa diintegralkan secara langsung untuk memperoleh

Integral F(t) dt, dinamakan impuls.Ini akan sama dengan perubahan momentum yang diberikan oleh suatu gaya F(t)yang bekerja pada suatu benda pada interval waktu tertentu. ( Ini bisa kita rubah dengan nilai awal dari t sampai t₀).

Kedudukan/posisi suatu partikel sebagai sebuah fungsi waktu bisa diperoleh dengan mengintegralkan dua kali F(t),

Gaya sebagai fungsi kecepatan

Sering terjadi bahwa gaya yang terjadi pada sebuah benda merupakan fungsi dari kecepatan benda. Contoh nyata, yaitu pada kasus hambatan viskositas yang bekerja pada benda yang brgerak dalam fluida. Jika gaya dapat dinyatakan hanya sebagai fungsi kecepatan saja:

gerak melingkar beraturan (GMB)

Gerak Melingkar Beraturan (GMB) adalah gerakan dalam lintasan berbentuk lingkaran dengan percepatan sudut tetap.

Beberapa lambang yang biasa ditemukan dalam GMB antara lain :

Frekuensi (f) dan periode (T) dalam GMB :

 sesuai dengan keterangan lambang2 di atas berarti :

Frekuensi = banyaknya putaran/waktu

Periode = waktu/banyaknya putaran

Rumus Kecepatan Sudut (ω)

 


 



Keterangan :
ω = Kecepatan sudut (rad/s)
f   = frekuensi (Hz)
T  = periode (s)
π  = 3,14 atau 22/7 atau tetap/tidak diganti angka


Hubungan Kecepatan Sudut dan Kecepatan Linear :

Keterangan :
ω = Kecepatan sudut (rad/s)
v  = Kecepatan linear (m/s)
r  = jari-jari lintasan (m) 

Percepatan dan Gaya Sentripetal :

percepatan sentripetal merupakan percepatan benda menuju pusat lingkaran....adanya percepatan ini menimbulkan gaya sentripetal.

Benda Yang Diputar Horizontal

mempunyai kecepatan maksimum (vmaks) yang dibatasi oleh tegangan tali maksimum (Tmaks) agar talinya tidak sampai putus.

AyunanKerucut (Konis)

Rumus-rumus dalam ayunan kerucut :

Kelajuan maksimum agar kendaraan membelok dengan baik

Sudut Kemiringan Jalan pada Belokan :

Pentiiing......

penggunaan rumus diatas ketika yang diketahui atai yang ditanyakan adalah kecepatan liniernya....namun bila yang diketahui adalah kecepatan sudutnya maka bagian rumus dibawah ini berubah menjadi....

pada pembahasan selanjutnya kecepatan yang dipakai adalah kecepatan linear......bila ada soal yang menggunakan kecepatan sudut cukup mengganti bagian yan ditampilkan di atas.

Gerak Melingkar Vertikal pada Seutas Tali

coba kalian perhatikan gaya2 yang bekerja pada bandul di setiap titiknya.....bila menuju pusat lingkaran bernilai positif sedangkan yang menjauhi pusat bernilai negatif. pada setiap titik tegangan tali (T) selalu menuju pusat lingkaran...sehingga harganya selalu ditulis positif. Kemudian berat bandul di titik A berarah menjauhi pusat lingkaran sehingga bernilai negatif, berat bandul di titik B tegak lurus dengan tali sehingga tidak memengaruhi besarnya tegangan tali atau bernilai nol (0) dan titik C berat bandul menuju pusat lingkaran sehingga bernilai positif.....dengan melihat pengaruh berat benda pada titik sembarang....misalnya titik P.....terlihat berat benda yang mempengaruhi tegangan tali sesuai dengan  perkalian berat bandul dengan nilai Cos sudut dengan acuan titik A....penggabungan besarnya tegangan dan pengaruh berat bandul setara dengan gaya sentripetal benda (Fs).

maka tegangan tali dapat kita cari dengan memindahkan pengaruh berat benda ke ruas kanan.....

kedua rumus di atas sebenarnya sama persis....hanya terjadi peruraian rumus saja terserah yang akan kalian hafal yang mana...bila sudah tahu prinsipnya sebenarnya tidak harus dihafal. sedangkan rumus2 khusus di beberapa titik sebagai berikut :

kecepatan minimum untuk.....

Gerak Melingkar Vertikal dalam Lingkaran

berbeda dengan gerak vertikal benda yang diikat dengan seutas tali......pada gerakan ini benda bergerak di dalam lintasan lingkaran yang vertikal atau dapat juga tempat berpijak bendalah yang berputar vertikal sementara benda tersebut berada di sebelah dalamnya....seperti air dalam ember yang diikat tali...atau pilot pesawat yang bermanuver membentuk lingkaran vertikal....atau seperti contoh gambar di atas (bola dalam ember). dalam kondisi ini berlaku rumus umum :

kecepatan minimal agar saat di titik tertinggi benda tidak meninggalkan lintasan.....

Gerakan Melingkar Vertikal di Luar Lingkaran

contoh gerakan ini adalah ketika sebuah kendaraan melintasi jalan yang gundukannya membentuk lingkaran....

coba kalian perhatikan....mengapa berat benda dikalikan dengan sin...dan bukannya cos.... alasannya terlihat dalam penguraian gaya berat pada gambar.... sehingga rumus umumnya :

saat di puncak berlaku.....

bahasan terakhir kita mengenai....

Hubungan Roda - roda

 

• Jika roda-roda sama pusatnya maka kecepatan sudutnya sama....dengan kecepatan sudut yang sama maka dapat kita cari kecepatan linier salah satu roda jika kecepatan linier roda yang lainnya diketahui.
• Jika roda-roda sama lintasannya maka kecepatan liniernya sama....dengan kecepatan linier yang sama maka dapat kita cari kecepatan sudut salah satu roda jika kecepatan sudut roda yang lainnya diketahui.

SELAMAT BELAJAR

contoh soal dan pembahasan tentang GLB dan GLBB

Soal No. 1
Batu bermassa 200 gram dilempar lurus ke atas dengan kecepatan awal 50 m/s.



Jika percepatan gravitasi ditempat tersebut adalah 10 m/s², dan gesekan udara diabaikan, tentukan :
a) Tinggi maksimum yang bisa dicapai batu
b) Waktu yang diperlukan batu untuk mencapai ketinggian maksimum
c) Lama batu berada diudara sebelum kemudian jatuh ke tanah

Pembahasan

a) Saat batu berada di titik tertinggi, kecepatan batu adalah nol dan percepatan yang digunakan adalah percepatan gravitasi. Dengan rumus GLBB:



b) Waktu yang diperlukan batu untuk mencapai titik tertinggi:



c) Lama batu berada di udara adalah dua kali lama waktu yang diperlukan untuk mencapai titik tertinggi.

t = (2)(5) = 10 sekon

Soal No. 2
Sebuah mobil bergerak dengan kelajuan awal 72 km/jam kemudian direm hingga berhenti pada jarak 8 meter dari tempat mulainya pengereman. Tentukan nilai perlambatan yang diberikan pada mobil tersebut!

Pembahasan
Ubah dulu satuan km/jam menjadi m/s kemudian gunakan persamaan untuk GLBB diperlambat:



Soal No. 3
Perhatikan grafik berikut ini.



Dari grafik diatas tentukanlah:
a. jarak tempuh gerak benda dari t = 5 s hingga t = 10 s
b. perpindahan benda dari t = 5 s hingga t = 10 s

Pembahasan
Jika diberikan graik V (kecepatan) terhadap t (waktu) maka untuk mencari jarak tempuh atau perpindahan cukup dari luas kurva grafik V-t. Dengan catatan untuk jarak, semua luas bernilai positif, sedang untuk menghitung perpindahan, luas diatas sumbu t bernilai positif, di bawah bernilai negatif.



Soal No. 4
Seekor semut bergerak dari titik A menuju titik B pada seperti terlihat pada gambar berikut.



Jika r = 2 m, dan lama perjalanan semut adalah 10 sekon tentukan:
a) Kecepatan rata-rata gerak semut
b) Kelajuan rata-rata gerak semut

Pembahasan
Terlebih dahulu tentukan nilai perpindahan dan jarak si semut :
Jarak yang ditempuh semut adalah dari A melalui permukaan lengkung hingga titik B, tidak lain adalah seperempat keliling lingkaran.
Jarak = ¹/₄ (2πr) = ¹/₄ (2π x 2) = π meter

Perpindahan semut dilihat dari posisi awal dan akhirnya , sehingga perpindahan adalah dari A tarik garis lurus ke B. Cari dengan phytagoras.
Perpindahan = √ ( 2² + 2² ) = 2√2 meter.

a) Kecepatan rata-rata = perpindahan : selang waktu
Kecepatan rata-rata = 2√2 meter : 10 sekon = 0,2√2 m/s

b) Kelajuan rata-rata = jarak tempuh : selang waktu
Kelajuan rata- rata = π meter : 10 sekon = 0,1 π m/s

Soal No. 5
Pesawat Burung Dara Airlines berangkat dari kota P menuju arah timur selama 30 menit dengan kecepatan konstan 200 km/jam. Dari kota Q berlanjut ke kota R yang terletak 53^o terhadap arah timur ditempuh selama 1 jam dengan kecepatan konstan 100 km/jam.

Tentukan:
a) Kecepatan rata-rata gerak pesawat
b) Kelajuan rata-rata gerak pesawat

Pembahasan
Salah satu cara :
Terlebih dahulu cari panjang PQ, QR, QR', RR', PR' dan PR



PQ = V_PQ x t_PQ = (200 km/jam) x (0,5) jam = 100 km
QR = V_QR x t_QR = (100 km/jam) x (1 jam) = 100 km
QR' = QR cos 53^o = (100 km) x (0,6) = 60 km
RR' = QR sin 53^o = (100 km) x (0,8) = 80 km
PR' = PQ + QR' = 100 + 60 = 160 km

PR = √[ (PR' )² + (RR')² ]
PR = √[ (160 ) ² + (80)² ] = √(32000) = 80√5 km

Jarak tempuh pesawat = PQ + QR = 100 + 100 = 200 km
Perpindahan pesawat = PR = 80√5 km
Selang waktu = 1 jam + 0,5 jam = 1,5 jam

a) Kecepatan rata-rata = perpindahan : selang waktu = 80√5 km : 1,5 jam = 53,3 √5 km/jam
b) Kelajuan rata-rata = jarak : selang waktu = 200 km : 1,5 jam = 133,3 km/jam

Soal No. 6
Diberikan grafik kecepatan terhadap waktu seperti gambar berikut:



Tentukan besar percepatan dan jenis gerak dari:
a) A - B
b) B - C
c) C - D

Pembahasan
Mencari percepatan (a) jika diberikan grafik V-t :

a = tan θ

dengan θ adalah sudut kemiringan garis grafik terhadap horizontal dan tan suatu sudut adalah sisi depan sudut dibagi sisi samping sudut. Ingat : tan-de-sa

a) A - B
a = (2 − 0) : (3− 0) = ²/₃ m/s²
(benda bergerak lurus berubah beraturan / GLBB dipercepat)
b) B - C
a = 0 (garis lurus, benda bergerak lurus beraturan / GLB)
c) C - D
a = (5 − 2) : (9 − 7) = ³/₂ m/s²
(benda bergerak lurus berubah beraturan / GLBB dipercepat)

Soal No. 7
Dari gambar berikut :



Tentukan:
a) Jarak tempuh dari A - B
b) Jarak tempuh dari B - C
c) Jarak tempuh dari C - D
d) Jarak tempuh dari A - D

Pembahasan
a) Jarak tempuh dari A - B
Cara Pertama
Data :
V_o = 0 m/s
a = (2 − 0) : (3− 0) = ²/₃ m/s²
t = 3 sekon
S = V_o t + ¹/₂ at²
S = 0 + ¹/₂ (²/₃ )(3)² = 3 meter

Cara Kedua
Dengan mencari luas yang terbentuk antara titik A, B dang angka 3 (Luas Segitiga = setengah alas x tinggi) akan didapatkan hasil yang sama yaitu 3 meter

b) Jarak tempuh dari B - C
Cara pertama dengan Rumus GLB
S = Vt
S = (2)(4) = 8 meter

Cara kedua dengan mencari luas yang terbentuk antara garis B-C, angka 7 dan angka 3 (luas persegi panjang)

c) Jarak tempuh dari C - D
Cara Pertama
Data :
V_o = 2 m/s
a = ³/₂ m/s²
t = 9 − 7 = 2 sekon
S = V_o t + ¹/₂ at²
S = (2)(2) + ¹/₂ (³/₂ )(2)²= 4 + 3 = 7 meter

Cara kedua dengan mencari luas yang terbentuk antara garis C-D, angka 9 dan angka 7 (luas trapesium)

S = 1/2 (jumlah sisi sejajar) x tinggi
S = 1/2 (2+5)(9-7) = 7 meter.

d) Jarak tempuh dari A - D
Jarak tempuh A-D adalah jumlah dari jarak A-B, B-C dan C-D

Soal No. 8
Mobil A dan B dalam kondisi diam terpisah sejauh 1200 m.



Kedua mobil kemudian bergerak bersamaan saling mendekati dengan kecepatan konstan masing-masing V_A = 40 m/s dan V_B = 60 m/s.
Tentukan:
a) Jarak mobil A dari tempat berangkat saat berpapasan dengan mobil B
b) Waktu yang diperlukan kedua mobil saling berpapasan
c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A

Pembahasan
Waktu tempuh mobil A sama dengan waktu tempuh mobil B, karena berangkatnya bersamaan. Jarak dari A saat bertemu misalkan X, sehingga jarak dari B (1200 − X)

t_A = t_B
^S_A/_VA = ^S_B/_VB
^{( x )}/₄₀ = ^{( 1200 − x )} /₆₀
6x = 4( 1200 − x )
6x = 4800 − 4x
10x = 4800
x = 480 meter

b) Waktu yang diperlukan kedua mobil saling berpapasan
x = V_A t
480 = 40t
t = 12 sekon

c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A
S_B =V_B t = (60) (12) = 720 m

Soal No. 9
Diberikan grafik kecepatan terhadap waktu dari gerak dua buah mobil, A dan B.



Tentukan pada jarak berapakah mobil A dan B bertemu lagi di jalan jika keduanya berangkat dari tempat yang sama!

Pembahasan
Analisa grafik:
Jenis gerak A → GLB dengan kecepatan konstan 80 m/s
Jenis gerak B → GLBB dengan percepatan a = tan α = 80 : 20 = 4 m/s²

Kedua mobil bertemu berarti jarak tempuh keduanya sama, misal keduanya bertemu saat waktu t
S_A = S_B
V_A t =V_oB t + ¹/₂ at²
80t = (0)t + ¹/₂ (4)t²
2t² − 80t = 0
t² − 40t = 0
t(t − 40) = 0
t = 0 sekon atau t = 40 sekon
Kedua mobil bertemu lagi saat t = 40 sekon pada jarak :
S_A = V_A t = (80)(40) = 3200 meter

Soal No. 10 (Gerak Vertikal ke Bawah / Jatuh Bebas)
Sebuah benda jatuh dari ketinggian 100 m. Jika percepatan gravitasi bumi 10 m/s²tentukan:
a) kecepatan benda saat t = 2 sekon
b) jarak tempuh benda selama 2 sekon
c) ketinggian benda saat t = 2 sekon
d) kecepatan benda saat tiba di tanah
e) waktu yang diperlukan benda hingga tiba di tanah

Pembahasan
a) kecepatan benda saat t = 2 sekon
Data :
t = 2 s
a = g = 10 m/s²
V_o = 0 m/s
V_t = .....!

V_t = V_o + at
V_t = 0 + (10)(2) = 20 m/s

c) jarak tempuh benda selama 2 sekon
S = V_ot + ¹/₂at²
S = (0)(t) + ¹/₂ (10)(2)²
S = 20 meter

c) ketinggian benda saat t = 2 sekon
ketinggian benda saat t = 2 sekon adalah tinggi mula-mula dikurangi jarak yang telah ditempuh benda.
S = 100 − 20 = 80 meter

d) kecepatan benda saat tiba di tanah
V_t² = V_o² + 2aS
V_t² = (0) + 2 aS
V_t = √(2aS) = √[(2)(10)(100)] = 20√5 m/s

e) waktu yang diperlukan benda hingga tiba di tanah
V_t = V₀ + at
20√5 = (0) + (10) t
t = 2√5 sekon

Soal No. 11

Besar kecepatan suatu partikel yang mengalami perlambatan konstan ternyata berubah dari 30 m/s menjadi 15 m/s setelah menempuh jarak sejauh 75 m. Partikel tersebut akan berhenti setelah menempuh jarak....
A. 15 m
B. 20 m
C. 25 m
D. 30 m
E. 50 m
(Soal SPMB 2003)

Pembahasan
Data pertama:
Vo = 30 m/s
Vt = 15 m/s
S = 75 m

Dari ini kita cari perlambatan partikel sebagai berikut:
Vt² = Vo² − 2aS
15² = 30² − 2a(75)
225 = 900 − 150 a
150 a = 900 − 225
a = 675 /150 = 4, 5 m/s²

Besar perlambatannya adalah 4,5 m/s² (Kenapa tidak negatif? Karena dari awal perhitungan tanda negatifnya sudah dimasukkan ke dalam rumus, jika ingin hasil a nya negatif, gunakan persamaan Vt² = Vo²+ 2aS)

Data berikutnya:
Vo = 15 m/s
Vt = 0 m/s (hingga berhenti)

Jarak yang masih ditempuh:

Vt²= Vo² − 2aS
0² = 15² − 2(4,5)S
0 = 225 − 9S
9S = 225

S = 225/9 = 25 m

Soal No. 12

Sebuah benda dijatuhkan dari ujung sebuah menara tanpa kecepatan awal. Setelah 2 detik benda sampai di tanah (g = 10 m s²). Tinggi menara tersebut …
A. 40 m
B. 25 m
C. 20 m
D. 15 m
E. 10 m
(EBTANAS 1991)


Pembahasan
Data:
ν_o = 0 m/s (jatuh bebas)
t = 2 s
g = 10 m s²
S = .....!

S = ν_o t + 1/2 gt²
S = (0)(2) + 1/2 (10)(2)²
S = 5(4) = 20 meter

Soal No. 13
Sebuah benda dijatuhkan dari ketinggian h di atas tanah. Setelah sampai di tanah kecepatannya 10 m s^–1, maka waktu yang diperlukan untuk mencapai ketinggian ¹/₂ h dari tanah (g = 10 m. s⁻²) adalah.....
A. 1/2 √2 sekon
B. 1 sekon
C. √2 sekon
D. 5 sekon
E. 5√2 sekon
(Soal Ebtanas 2002)

Pembahasan
Data:
Untuk jarak tempuh sejauh S₁ = h
ν_o = 0 ms^–1
ν_t = 10 m s^–1

ν_t= ν_o + at
10 = 0 + 10t
t = 1 sekon -> t₁

Untuk jarak tempuh sejauh S₂ = ¹/₂ h
t₂ =......


Perbandingan waktu tempuh:

Soal No. 14
Sebuah batu dijatuhkan dari puncak menara yang tingginya 40 m di atas tanah. Jika g = 10 m s^–2, maka kecepatan batu saat menyentuh tanah adalah.…
A. 20√2 m s^–1
B. 20 m s^–1
C. 10√2 m s^–1
D. 10 m s^–1
E. 4√2 m s^–1
(Ebtanas Fisika 1996)

Pembahasan
Jatuh bebas, kecepatan awal nol, percepatan a = g = 10 m s^–2

Soal No. 15

Mobil massa 800 kg bergerak lurus dengan kecepatan awal 36 km.jam^–1setelah menempuh jarak 150 m kecepatan menjadi 72 km. jam^–1. Waktu tempuh mobil adalah...
A. 5 sekon
B. 10 sekon
C. 17 sekon
D. 25 sekon
E. 35 sekon
(Ujian Nasional 2009)

Pembahasan
Data soal:
m = 800 kg
ν_o = 36 km/jam = 10 m/s
ν_t = 72 km/jam = 20 m/s
S = 150 m
t = ..........

Tentukan dulu percepatan gerak mobil (a) sebagai berikut:
ν_t² = ν_o² + 2aS
20² = 10² + 2a(150)
400 = 100 + 300 a
400 − 100 = 300 a
300 = 300 a
a = ³⁰⁰/₃₀₀ = 1 m/s²

Rumus kecepatan saat t:
ν_t = ν_o + at
20 = 10 + (1)t
t = 20 − 10 = 10 sekon

Catatan:
Massa mobil (m) tidak diperlukan dalam perhitungan, apalagi merknya.